ITパスポートのテクノロジ分野の「基数変換」について紹介します。テクノロジ系の問題の中で計算問題がありますので、計算の仕方を覚えておきましょう!
基数変換とは?
基数変換(きすうへんかん)とは、ある数の表記法(基数)から別の表記法へと変換することです。一般的には、10進数(デシマル)から2進数(バイナリ)、8進数、16進数などへの変換がよく知られています。
ITパスポートの試験では「2進数」「16進数」の計算問題が登場します!
計算方法
10進数の数を2進数に変換する場合、数を2で割りながら余りを求めていき、その余りを逆順に並べていくことで2進数を得ることができます。同様に、16進数に変換する際も、それぞれの基数に合わせた計算方法があります。
その逆もあります。16進数を10進数に変換する問題もあるということです。
10進数の概念
10進数(英:decimal)は、0から9までの10種類の数字を使用して数を表現する数の体系です。これは、日常的に最も広く使われている数の表現方法です。
10進数の基数は10です。これは、0から9までの10個の数字を使うことを意味します。
10進数の起源は古代にさかのぼり、主に人間の手指が10本であることに由来します。これは、数を数えるのに便利であったためと考えられているそうです。

2進数の概念

2進数(英:binary)は、数を表すために2つの数字、すなわち0と1のみを使用する数の表記法です。これはコンピュータの内部で情報を表現するために広く用いられています。0、1の次で桁上がりします。
2進数の各桁はビット(bit)と呼ばれ、0または1のどちらかであり、2進数の最小単位です。2進数では、各桁の位置は2の累乗に対応します。
2進数を10進数へ基数変換
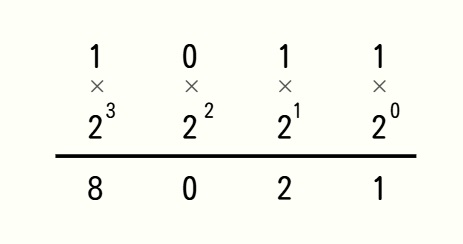
たとえば、2進数の 1011 を10進数へ基数変換すると、上記のようになります。 1×(2の3乗)というように計算してください。
8+0+2+1 = 11
2進数「1011」の10進数は「11」ということです。
16進数の概念

16進数(英:hexadecimal)は、基数16の数体系であり、0から9までの数字と、AからFまでの6つのアルファベットを使用して数を表現します。Fの次で桁上りします。
16進数を10進数へ基数変換
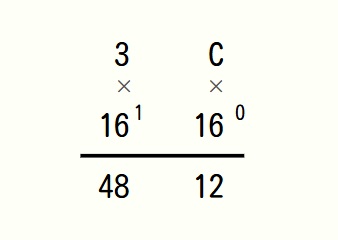
たとえば、16進数の 3C を10進数へ基数変換すると、上記のようになります。
Cは、10進数で「12」を指します。48+12=60
16進数「3C」の10進数は「60」ということです。
まとめ
基数変換は、コンピュータ科学で重要な概念であり、データのビット操作や符号化、データ通信などの分野で広く利用されています。ただ計算方法を覚えるだけで、4択から選ぶので特に難しくないと思います。
自分で何度か例を出して解いてみてください。
